PMF, PDF, and CDF

Let’s start this with the question:

What are random variables when it comes to statistics and probability?

A random variable can be defined as a variable that holds a set of possible values from an experiment.

Random variable can be further classified as:

1. Discreet: Can take up only finite number of values (rolling a dice)

2. Continuous: Can take up any value within a range (Weight & height of a person)

Now, since the focus for today is on probability distributions - let’s understand what is a probability distribution?

A probability distribution can be defined as a distribution depicting the likelihood of different outcomes of an experiment.

What does a probability distribution look like?

Before we answer that, let’s understand the type of probability distributions that exit. Since a probability distribution depicts the likelihood of the outcomes of an experiment and those outcomes can be of two type - discrete & continuous - therefore, the distribution would be of two types as well:

1. Discrete probability distribution

2. Continuous probability distribution

Now we can discuss what these probability distributions look like. The probability distribution for a discrete variable is described by Probability Mass Function (PMF) whereas the probability distribution of continuous variable are described by Probability Distribution Function (PDF).

Cumulative Probability Distribution (CDF): Probability distribution shows the probability of a point whereas the CDF shows the probability of everything up until that point.

Let’s demonstrate these distributions through examples in python:

1. Discrete probability distribution (PMF)

   

   Y-axis in case of PMF shows the probability of the corresponding x-value

2. Continuous probability distribution (PDF)

   

   Y axis in case of PDF shows the density of the corresponding x-value

   

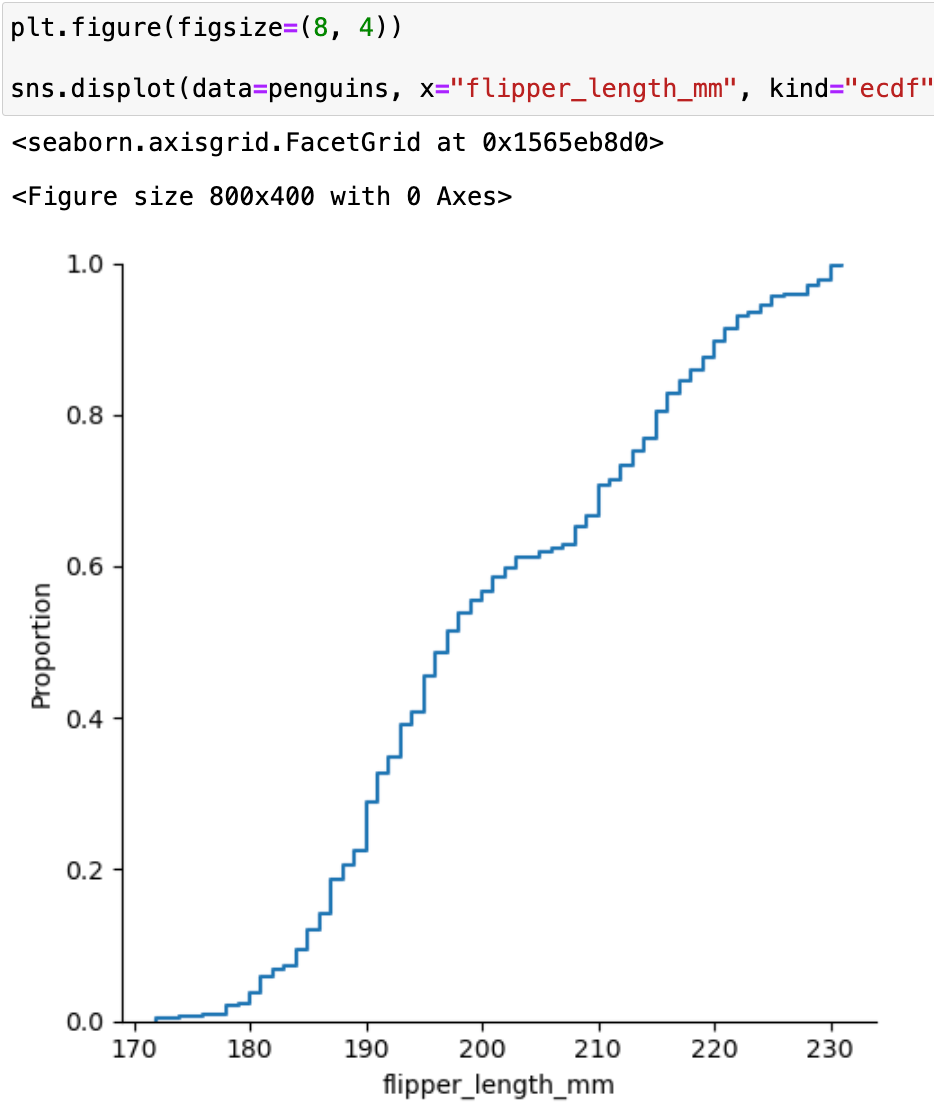
   CDF from PDF

The cumulative distribution plotted from PMF & PDF both shows that the cumulative probability add up to 1 as the value of x keeps on increasing & at a particular point the cumulative probability is equal to less than x, i.e., F(x) = P[X<=x]